¿Alguna vez te has preguntado por qué una pelota rebota al caer al suelo o cómo funciona una montaña rusa? La respuesta está en los conceptos de energía cinética y potencial, dos formas fundamentales de energía mecánica que explican gran parte de los fenómenos físicos que observamos en nuestro día a día.

En mis más de 15 años como profesora de secundaria, he comprobado que estos conceptos suelen generar confusión entre el alumnado. Sin embargo, son esenciales para comprender desde la física básica hasta problemas más complejos en cursos superiores. Por eso, he decidido crear esta guía práctica que te ayudará a entender qué son estas energías y, sobre todo, cómo calcularlas correctamente.

La energía cinética es la energía que posee un cuerpo debido a su movimiento. Esta forma de energía depende tanto de la masa del objeto como de su velocidad. Cuanto mayor sea la masa o la velocidad de un objeto, mayor será su energía cinética.

Para entenderlo mejor, pensemos en situaciones cotidianas: un coche en movimiento tiene energía cinética, así como una pelota lanzada, una persona corriendo o incluso las moléculas de aire que nos rodean. Todos estos ejemplos ilustran cómo la energía cinética está presente en prácticamente todos los movimientos que observamos.

La energía cinética se mide en julios (J) en el Sistema Internacional de Unidades, aunque a veces también podemos encontrarla expresada en calorías o kilovatios-hora dependiendo del contexto.

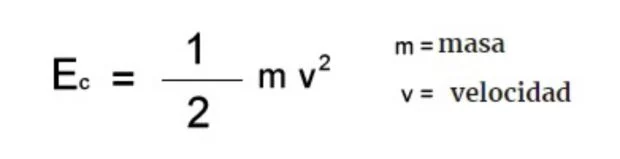
Fórmula para calcular la energía cinética

La fórmula para calcular la energía cinética (Ec) es:

Ec = ½ · m · v²

Donde:

• m es la masa del objeto (en kilogramos)
• v es la velocidad del objeto (en metros por segundo)
• Ec es la energía cinética (en julios)

Es importante observar que la energía cinética depende de la velocidad al cuadrado, lo que significa que si duplicamos la velocidad, la energía cinética se multiplicará por cuatro. Esta relación no lineal explica por qué a altas velocidades, los objetos tienen mucha más energía de lo que podríamos intuir.

Ejemplos resueltos de cálculo de energía cinética

Ejemplo 1: Cálculo básico

Calculemos la energía cinética de un coche de 1.500 kg que se mueve a una velocidad de 72 km/h.

Paso 1: Convertir las unidades al Sistema Internacional. Necesitamos pasar los km/h a m/s: 72 km/h = 72 × (1.000/3.600) = 20 m/s

Paso 2: Aplicar la fórmula de la energía cinética: Ec = ½ · m · v² Ec = ½ · 1.500 kg · (20 m/s)² Ec = ½ · 1.500 kg · 400 m²/s² Ec = 300.000 J = 300 kJ

El coche tiene una energía cinética de 300 kJ.

Ejemplo 2: Comparación de energías cinéticas

Comparemos la energía cinética de dos objetos:

• Una bala de 10 gramos que viaja a 400 m/s
• Una pelota de tenis de 57 gramos que se mueve a 30 m/s

Para la bala: Ec = ½ · 0,01 kg · (400 m/s)² = ½ · 0,01 kg · 160.000 m²/s² = 800 J

Para la pelota: Ec = ½ · 0,057 kg · (30 m/s)² = ½ · 0,057 kg · 900 m²/s² = 25,65 J

¡La bala tiene más de 30 veces la energía cinética de la pelota, a pesar de tener menos masa! Esto demuestra claramente la importancia de la velocidad en el cálculo de la energía cinética.

¿Qué es la energía potencial?

La energía potencial es la energía almacenada en un cuerpo debido a su posición o configuración. A diferencia de la energía cinética, la energía potencial es una energía «en potencia», que puede transformarse en energía cinética bajo ciertas condiciones.

Existen diferentes tipos de energía potencial, pero en la física de secundaria y bachillerato nos centramos principalmente en dos:

1. Energía potencial gravitatoria: relacionada con la altura de un objeto en un campo gravitatorio
2. Energía potencial elástica: asociada a la deformación de un cuerpo elástico, como un muelle o un resorte

La energía potencial también se mide en julios (J) en el Sistema Internacional.

Energía potencial gravitatoria: fórmula y cálculo

La energía potencial gravitatoria (Epg) es la energía que posee un objeto debido a su altura respecto a un nivel de referencia en un campo gravitatorio. Se calcula mediante la siguiente fórmula:

Epg = m · g · h

Donde:

• m es la masa del objeto (en kilogramos)
• g es la aceleración de la gravedad (aproximadamente 9,8 m/s² en la superficie terrestre)
• h es la altura sobre el nivel de referencia (en metros)
• Epg es la energía potencial gravitatoria (en julios)

Es importante destacar que el nivel de referencia es arbitrario. Podemos elegirlo en función del problema concreto que estemos resolviendo. Lo habitual es tomar como referencia (h = 0) el suelo, la superficie terrestre o el punto más bajo de la trayectoria del objeto.

Ejemplo de cálculo de energía potencial gravitatoria

Calculemos la energía potencial gravitatoria de un libro de 0,5 kg que se encuentra en una estantería a 2 metros del suelo.

Aplicando la fórmula: Epg = m · g · h Epg = 0,5 kg · 9,8 m/s² · 2 m Epg = 9,8 J

El libro tiene una energía potencial gravitatoria de 9,8 J respecto al suelo.

Si ahora cambiamos nuestro nivel de referencia y lo situamos a 1 metro del suelo, la nueva altura del libro sería h = 1 m, y su energía potencial: Epg = 0,5 kg · 9,8 m/s² · 1 m = 4,9 J

Este ejemplo ilustra claramente cómo el valor de la energía potencial depende del nivel de referencia elegido, algo que a menudo confunde a mis estudiantes.

Energía potencial elástica: fórmula y cálculo

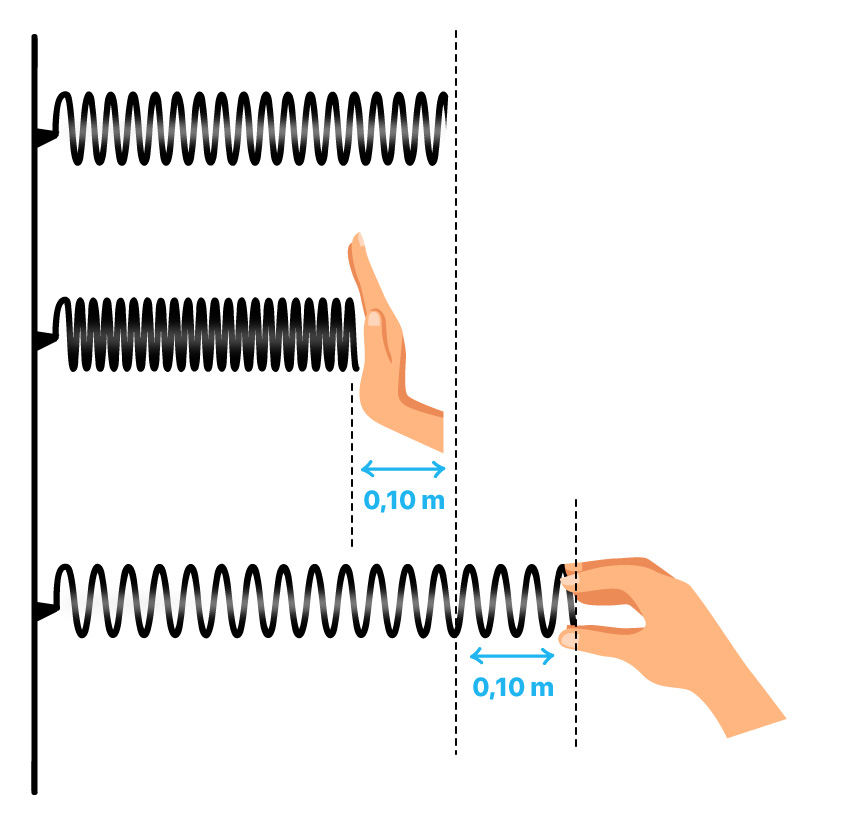
La energía potencial elástica (Epe) es la energía almacenada en un objeto elástico (como un muelle) cuando se deforma. Se calcula mediante la siguiente fórmula:

Epe = ½ · k · x²

Donde:

• k es la constante elástica del muelle (en N/m)
• x es la deformación del muelle respecto a su posición de equilibrio (en metros)
• Epe es la energía potencial elástica (en julios)

Nótese la semejanza con la fórmula de la energía cinética. En ambos casos aparece un factor ½ y una magnitud al cuadrado. Esta similitud no es causalidad, sino que refleja propiedades fundamentales de la física.

Ejemplo de cálculo de energía potencial elástica

Supongamos que tenemos un muelle con una constante elástica k = 200 N/m y lo estiramos 15 cm desde su posición de equilibrio. Calculemos su energía potencial elástica.

Paso 1: Convertir la deformación a metros: x = 15 cm = 0,15 m

Paso 2: Aplicar la fórmula: Epe = ½ · k · x² Epe = ½ · 200 N/m · (0,15 m)² Epe = ½ · 200 N/m · 0,0225 m² Epe = 2,25 J

El muelle deformado almacena 2,25 J de energía potencial elástica.

Conservación de la energía mecánica

Uno de los principios más importantes de la física es el principio de conservación de la energía mecánica. Este principio establece que, en ausencia de fuerzas disipativas (como el rozamiento), la suma de la energía cinética y la energía potencial de un sistema se mantiene constante.

Matemáticamente: Ec + Ep = constante

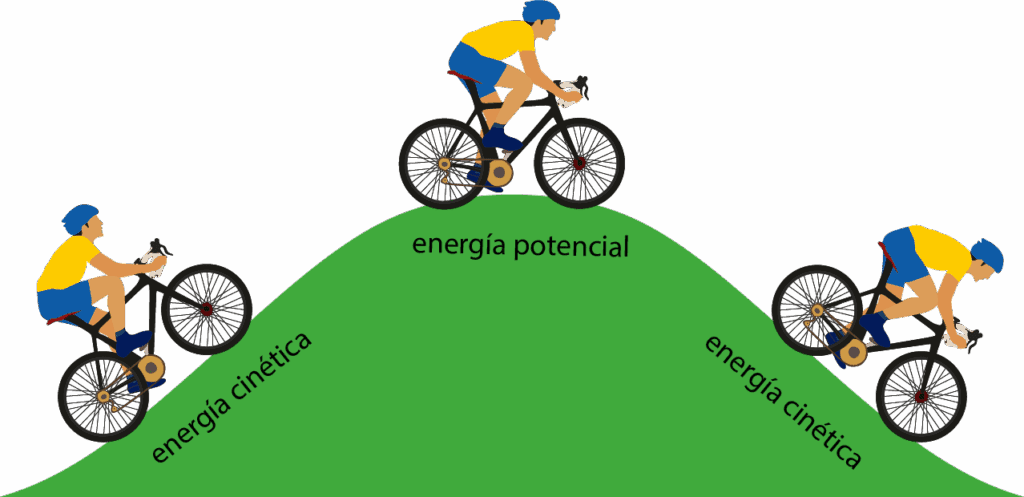
Esto significa que la energía no se crea ni se destruye, sino que se transforma de un tipo a otro. Por ejemplo, cuando lanzamos una pelota hacia arriba:

1. Al inicio, la pelota tiene principalmente energía cinética (está en movimiento)
2. A medida que sube, la energía cinética disminuye y la energía potencial aumenta
3. En el punto más alto, toda la energía cinética se ha transformado en energía potencial (la velocidad es cero)
4. Durante la caída, la energía potencial se convierte nuevamente en energía cinética

Este principio es fundamental para resolver muchos problemas de física y entender numerosos fenómenos naturales, desde el movimiento de los planetas hasta el funcionamiento de una montaña rusa.

Ejemplo de aplicación del principio de conservación

Supongamos que dejamos caer una pelota de 200 gramos desde una altura de 5 metros. ¿Cuál será su velocidad justo antes de tocar el suelo? Despreciamos el rozamiento con el aire.

Paso 1: Identificar la situación inicial y final.

• Inicial: La pelota está en reposo a 5 metros de altura (solo tiene energía potencial)
• Final: La pelota está a punto de tocar el suelo (solo tiene energía cinética)

Paso 2: Aplicar el principio de conservación de la energía mecánica. Ecinicial + Epinicial = Ecfinal + Epfinal

Paso 3: Sustituir los valores. 0 + m·g·h = ½·m·v² + 0 m·g·h = ½·m·v²

Paso 4: Despejar la velocidad final. v² = 2·g·h v = √(2·g·h) v = √(2·9,8·5) v ≈ 9,9 m/s

La pelota llegará al suelo con una velocidad aproximada de 9,9 m/s.

¡Vaya! Me acabo de dar cuenta de que no necesitábamos el valor de la masa para resolver este problema. Esto sucede porque, en caída libre, la aceleración es independiente de la masa del objeto. ¡Un detalle interesante que siempre sorprende a mis alumnos!

Aplicaciones prácticas

Los conceptos de energía cinética y potencial tienen numerosas aplicaciones en nuestra vida cotidiana y en la tecnología. Algunas de las más relevantes son:

Montañas rusas

Las montañas rusas son un ejemplo perfecto de la transformación entre energía potencial y cinética. Al inicio, el vagón es elevado a gran altura, acumulando energía potencial gravitatoria. Durante el descenso, esta energía se transforma en cinética, proporcionando la emocionante sensación de velocidad.

Generación de electricidad

En las centrales hidroeléctricas, se aprovecha la energía potencial del agua almacenada en presas. Al caer, esta energía se convierte en cinética y luego en eléctrica mediante turbinas y generadores.

Seguridad vial

El diseño de sistemas de seguridad en vehículos tiene muy en cuenta la energía cinética. Los airbags, cinturones y zonas de deformación están pensados para disipar la energía cinética en caso de colisión, reduciendo el impacto sobre los ocupantes.

Deportes

En muchos deportes como el salto con pértiga, el tenis o el golf, se aprovecha la transformación entre diferentes tipos de energía para maximizar el rendimiento. Por ejemplo, en el salto con pértiga, la energía cinética del atleta se transforma en elástica en la pértiga y luego en potencial al ganar altura.

Ejercicios propuestos

Para consolidar los conocimientos adquiridos, te propongo los siguientes ejercicios:

1. Un coche de 1.200 kg se mueve a una velocidad de 90 km/h. Calcula:
   • Su energía cinética
   • La energía cinética si duplicamos su velocidad
2. Una pelota de 300 gramos se lanza verticalmente hacia arriba con una velocidad inicial de 15 m/s. Calcula:
   • Su energía cinética inicial
   • La altura máxima que alcanzará (pista: en el punto más alto, la velocidad es cero)
   • Su energía potencial en el punto más alto
3. Un muelle de constante elástica k = 300 N/m se comprime 10 cm. Calcula:
   • La energía potencial elástica almacenada
   • Si soltamos el muelle y este impulsa una bola de 50 gramos, ¿qué velocidad adquirirá la bola? (suponiendo que toda la energía elástica se transforma en cinética)
4. Una montaña rusa tiene su punto más alto a 40 metros del suelo. Si un vagón de 500 kg parte del reposo desde esa altura, calcula:
   • La velocidad que tendrá al llegar al punto más bajo (despreciando rozamientos)
   • ¿Qué altura alcanzará en una subida posterior si en ese momento su velocidad es de 10 m/s?

Referencias bibliográficas

• Tipler, P. A., & Mosca, G. (2010). Física para la ciencia y la tecnología, Vol. 1: Mecánica, oscilaciones y ondas, termodinámica (6ª ed.). Editorial Reverté. https://www.reverte.com/libro/fisica-para-la-ciencia-y-la-tecnologia-i-6-ed_121640/
• Hewitt, P. G. (2004). Física conceptual (9ª ed.). Pearson Educación. https://www.pearsoneducacion.net/mexico/tienda-online/fisica-conceptual-1ed-hewitt-mx-epub
• Serway, R. A., & Jewett, J. W. (2018). Física para ciencias e ingeniería (10ª ed.). Cengage Learning. https://latam.cengage.com/libros/fisica-para-ciencias-e-ingenieria/
• Ministerio de Educación y Formación Profesional. (2020). Currículo de Física y Química para ESO y Bachillerato. https://www.educacionyfp.gob.es/contenidos/estudiantes/educacion-secundaria/informacion-general/curriculo.html
• Feynman, R. P., Leighton, R. B., & Sands, M. (2011). The Feynman Lectures on Physics, Vol. I: Mainly Mechanics, Radiation, and Heat. Basic Books. https://www.feynmanlectures.caltech.edu/I_toc.html
• Real Sociedad Española de Física. (2022). Revista Española de Física. https://revistadefisica.es/