¿Alguna vez te has preguntado por qué los antiguos griegos ya estaban fascinados con algo tan aparentemente simple como el movimiento en línea recta? O quizás, ¿por qué este tema sigue siendo la primera piedra sobre la que construimos todo el edificio de la física en los institutos españoles?

El Movimiento Rectilíneo Uniforme, ese viejo conocido que llamamos cariñosamente MRU, es mucho más que fórmulas para aprobar exámenes. Es la puerta de entrada a entender el universo. Y aunque pueda sonar grandilocuente, no exagero: desde los trenes de alta velocidad hasta las órbitas planetarias, todo comienza aquí.

En este artículo vamos a desentrañar sus secretos, explicar sus fórmulas de manera cristalina y, lo más importante, resolver paso a paso varios problemas para que puedas dominar este concepto fundamental. Tanto si eres estudiante de 4º de ESO como si estás preparándote para la EBAU, encontrarás aquí las herramientas que necesitas.

¿Qué es exactamente el MRU? Definición para no olvidar

El Movimiento Rectilíneo Uniforme es, sencillamente, aquel movimiento en el que un cuerpo:

• Se desplaza en línea recta (rectilíneo).
• Mantiene una velocidad constante (uniforme).

¡Así de simple! Pero no confundamos simple con trivial. Como diría mi profesor de física: «Lo más sencillo suele ser lo más profundo».

En términos más técnicos, estamos hablando de un movimiento donde la velocidad es un vector constante, tanto en módulo como en dirección y sentido. Esto implica que la aceleración es nula (a = 0 m/s²) y que la trayectoria es una línea recta perfecta.

Las ecuaciones fundamentales del MRU (que debes conocer)

Vamos al grano. Las fórmulas del MRU son relativamente sencillas, pero es crucial entender lo que cada símbolo representa:

Ecuación de la posición

x = x₀ + v·t

Donde:

• x = posición final (m)
• x₀ = posición inicial (m)
• v = velocidad (m/s)
• t = tiempo transcurrido (s)

Esta ecuación es la madre de todas las ecuaciones del MRU. Nos dice dónde estará un objeto en cualquier instante, conociendo su posición inicial y su velocidad.

Ecuación de la velocidad

v = Δx/Δt = (x – x₀)/t

Es decir, la velocidad es el cambio de posición dividido por el tiempo empleado. En el MRU esta velocidad es constante, lo que simplifica enormemente los cálculos.

Representación gráfica

El MRU tiene unas gráficas características que conviene reconocer a primera vista:

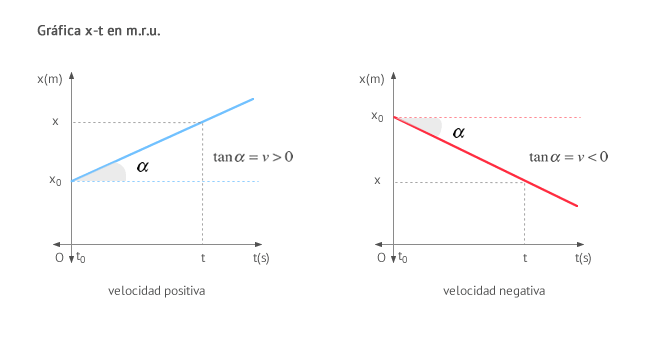
• Gráfica posición-tiempo (x-t): Es una línea recta cuya pendiente representa la velocidad.
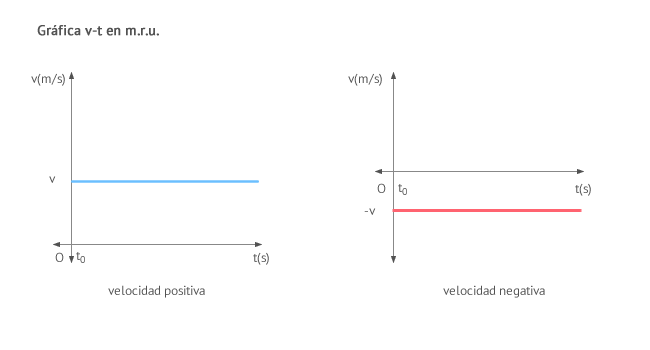
• Gráfica velocidad-tiempo (v-t): Es una línea horizontal paralela al eje del tiempo.
• Gráfica aceleración-tiempo (a-t): Es una línea horizontal coincidente con el eje del tiempo (a = 0).

¿Sabes interpretar estas gráficas? Si dominas este aspecto, tendrás medio examen ganado.

El MRU en la vida cotidiana: No todo es teoría

Antes de sumergirnos en los problemas, conviene reflexionar sobre dónde podemos observar el MRU en nuestra vida diaria. Aunque el MRU perfecto es una idealización (debido al rozamiento y otras fuerzas), hay ejemplos que se aproximan bastante:

• Un coche circulando por autopista con el control de crucero activado.
• El movimiento de las cintas transportadoras en los aeropuertos.
• Las escaleras mecánicas funcionando a velocidad constante.
• Un ascensor entre dos pisos (en la fase de velocidad constante).
• Una gota de lluvia que ha alcanzado su velocidad terminal.

Estos ejemplos nos ayudan a conectar la teoría con la realidad, algo fundamental para entender verdaderamente la física.

Problemas resueltos de MRU: Del concepto a la práctica

Vamos a resolver varios problemas de dificultad creciente. No te limites a memorizar los pasos; intenta entender la lógica detrás de cada operación.

Problema 1: El ciclista constante

Enunciado: Un ciclista recorre una carretera recta a una velocidad constante de 20 km/h. Si parte del kilómetro 5 de la carretera, ¿en qué punto se encontrará después de 2 horas?

Resolución: Lo primero es identificar los datos y pasarlos al Sistema Internacional:

• Velocidad: v = 20 km/h = 5,56 m/s.
• Posición inicial: x₀ = 5 km = 5.000 m.
• Tiempo: t = 2 h = 7.200 s.

Aplicamos la ecuación de posición del MRU: x = x₀ + v·t x = 5.000 m + 5,56 m/s · 7.200 s x = 5.000 m + 40.032 m x = 45.032 m = 45,03 km

Respuesta: El ciclista se encontrará en el kilómetro 45,03 de la carretera.

¿Has visto lo sencillo que resulta cuando tienes clara la ecuación básica? La clave está en mantener la coherencia en las unidades.

Problema 2: Encuentro en la carretera

Enunciado: Dos coches parten simultáneamente desde dos ciudades separadas por 200 km y viajan en MRU uno hacia el otro. Si el primer coche viaja a 90 km/h y el segundo a 110 km/h, ¿cuánto tiempo tardarán en encontrarse y a qué distancia de la primera ciudad ocurrirá el encuentro?

Resolución: Este problema es más complejo porque involucra dos móviles. Vamos paso a paso:

Datos:

• Distancia total: d = 200 km.
• Velocidad del primer coche: v₁ = 90 km/h.
• Velocidad del segundo coche: v₂ = 110 km/h.

Para calcular el tiempo de encuentro, consideramos que la suma de las distancias recorridas por ambos debe ser igual a la distancia total: v₁·t + v₂·t = d t·(v₁ + v₂) = d t = d/(v₁ + v₂) t = 200 km/(90 km/h + 110 km/h) t = 200 km/200 km/h t = 1 h

Para calcular la distancia desde la primera ciudad: x = v₁·t x = 90 km/h · 1 h x = 90 km

Respuesta: Los coches se encontrarán después de 1 hora, a 90 km de la primera ciudad.

Fíjate en cómo hemos usado la lógica más que las fórmulas memorizadas. Este enfoque de «sentido común físico» es el que realmente te ayudará en el examen.

Problema 3: Análisis de gráfica posición-tiempo

Enunciado: La siguiente gráfica posición-tiempo representa el movimiento de un objeto. Determina: a) La velocidad del objeto b) La ecuación del movimiento c) La posición del objeto cuando t = 5 s

[En una gráfica posición-tiempo, se observaría una línea recta que pasa por el punto (0, 2) y tiene pendiente positiva]

Resolución: De la gráfica podemos extraer:

• Posición inicial: x₀ = 2 m (corte con el eje y).
• Observando la gráfica, vemos que en t = 3 s, x = 8 m.

a) Calculamos la velocidad (pendiente de la recta): v = (x – x₀)/(t – t₀) = (8 m – 2 m)/(3 s – 0 s) = 6 m/3 s = 2 m/s.

b) La ecuación del movimiento será: x = x₀ + v·t x = 2 m + 2 m/s·t.

c) Posición en t = 5 s: x = 2 m + 2 m/s · 5 s = 2 m + 10 m = 12 m.

Respuesta: a) La velocidad es 2 m/s b) La ecuación es x = 2 + 2t (en metros y segundos) c) En t = 5 s, el objeto estará en x = 12 m

Las gráficas son una forma visual y potente de entender el movimiento. Aprender a interpretarlas correctamente te dará una ventaja enorme.

Problema 4: El tren y el peatón

Enunciado: Un tren parte de una estación con MRU a una velocidad de 72 km/h. Un peatón se encuentra caminando por un andén paralelo a las vías a 5 km de la estación, alejándose de ella a 4 km/h. ¿Cuánto tiempo tardará el tren en alcanzar al peatón? ¿A qué distancia de la estación ocurrirá?

Resolución: Primero, pasemos todo al mismo sistema de unidades (km y h):

• Velocidad del tren: vₜ = 72 km/h.
• Velocidad del peatón: vₚ = 4 km/h.
• Posición inicial del tren: x₀ₜ = 0 km.
• Posición inicial del peatón: x₀ₚ = 5 km.

Las ecuaciones de posición serán:

• Tren: xₜ = vₜ·t = 72t.
• Peatón: xₚ = x₀ₚ + vₚ·t = 5 + 4t.

En el momento del alcance, xₜ = xₚ: 72t = 5 + 4t 68t = 5 t = 5/68 h ≈ 0,0735 h ≈ 4,41 min.

La distancia desde la estación será: x = vₜ·t = 72 km/h · 0,0735 h = 5,29 km.

Respuesta: El tren alcanzará al peatón aproximadamente a los 4,41 minutos, a una distancia de 5,29 km de la estación.

En este problema vemos cómo dos movimientos rectilíneos uniformes interactúan. Este tipo de ejercicios son frecuentes en selectividad.

Aplicaciones prácticas del MRU en la ciencia y la tecnología

El MRU no es solo un tema académico; tiene aplicaciones prácticas en múltiples campos:

• Ingeniería de transportes: Cálculo de tiempos de llegada en sistemas de transporte.
• Astronomía: Aproximación inicial para estudiar el movimiento de cuerpos celestes.
• Robótica: Programación de movimientos básicos en robots.
• Física de partículas: Estudio del movimiento de partículas en aceleradores lineales.
• Aeronáutica: Cálculos de navegación en vuelo crucero.

Comprender el MRU es el primer paso para entender fenómenos físicos más complejos. Como dijo Isaac Newton: «Si he visto más lejos es porque estoy sentado sobre los hombros de gigantes». El MRU es uno de esos gigantes fundamentales.

¿Por qué es tan importante entender el MRU?

A estas alturas quizás te preguntes: «¿Tanto lío para algo tan simple como moverse en línea recta a velocidad constante?»

La respuesta es un rotundo SÍ. Y te explico por qué:

1. El MRU es la base conceptual sobre la que se construyen movimientos más complejos (MRUA, MCU, tiro parabólico…).
2. Desarrolla tu pensamiento analítico al relacionar magnitudes físicas básicas.
3. Te enseña a interpretar gráficas, una habilidad crucial en ciencias.
4. Es el primer caso en el que aplicamos ecuaciones diferenciales simplificadas (aunque no te lo expliquen así en secundaria).
5. Proporciona un modelo idealizado que sirve como aproximación a situaciones reales.

Mi profesor de física solía decir: «Quien no entiende el MRU, no entenderá la mecánica». Y tenía toda la razón.

Consejos para Resolver Problemas de MRU en Exámenes

Después de años explicando física, he notado que los estudiantes suelen cometer siempre los mismos errores. Aquí van algunos consejos:

1. Dibuja un esquema antes de empezar a resolver cualquier problema.
2. Establece un sistema de referencia claro (origen y sentidos positivo/negativo).
3. Convierte todas las unidades al Sistema Internacional antes de sustituir en las fórmulas.
4. Despeja algebraicamente antes de sustituir valores numéricos.
5. Comprueba si tu respuesta tiene sentido físico (¿es razonable ese resultado?).
6. Recuerda que los signos importan: indican dirección y sentido.

Siguiendo estos consejos, verás cómo tus notas en física mejoran considerablemente.

El MRU como base para entender el MRUA

Una vez dominado el MRU, el siguiente paso lógico es el Movimiento Rectilíneo Uniformemente Acelerado (MRUA), donde la aceleración es constante. La belleza de la física está en cómo cada concepto se construye sobre el anterior.

La comparación entre MRU y MRUA puede resumirse así:

Característica	MRU	MRUA
Aceleración	a = 0	a = constante ≠ 0
Velocidad	v = constante	v = v₀ + a·t
Posición	x = x₀ + v·t	x = x₀ + v₀·t + ½·a·t²
Gráfica x-t	Línea recta	Parábola
Gráfica v-t	Línea horizontal	Línea recta inclinada

Conclusión: El MRU como piedra angular

Hemos recorrido un largo camino desde la definición básica del Movimiento Rectilíneo Uniforme hasta la resolución de problemas complejos. Espero que ahora veas este tema con otros ojos: no como algo trivial, sino como el fundamento esencial de toda la mecánica clásica.

Como dijo el físico Richard Feynman: «La naturaleza utiliza solo las cuerdas más largas para tocar sus melodías; el resto son armonías». El MRU es una de esas cuerdas fundamentales que nos permite entender la sinfonía del movimiento.

La próxima vez que viajes en tren, mires las estrellas o simplemente camines por la calle, piensa en cómo el MRU está presente en cada uno de esos fenómenos. La física no está solo en los libros; está en cada aspecto de nuestra vida cotidiana.

Y recuerda: la clave del éxito en física no es memorizar fórmulas, sino entender conceptos. Si has comprendido el MRU, has dado un paso gigante en tu camino científico.

Referencias bibliográficas

Tipler, P. A., & Mosca, G. (2010). Física para la ciencia y la tecnología, Vol. 1: Mecánica, oscilaciones y ondas, termodinámica (6ª ed.). Editorial Reverté.

Pérez García, V. M., & Vázquez Martínez, L. (2015). Física Básica. Universidad Nacional de Educación a Distancia.

Hewitt, P. G. (2016). Física Conceptual (12ª ed.). Pearson Educación.

Sears, F. W., Zemansky, M. W., Young, H. D., & Freedman, R. A. (2018). Física Universitaria, Vol. 1 (14ª ed.). Pearson Educación.

Real Sociedad Española de Física. (2023). Revista Española de Física, Vol. 37(2). RSEF.

Fernández Sánchez, J. (2022). Cinemática: Movimiento rectilíneo uniforme y uniformemente acelerado. Proyecto Newton, INTEF.