¿Alguna vez te has preguntado por qué los objetos se mueven como lo hacen? ¿O por qué algunas cosas parecen más difíciles de empujar que otras a pesar de tener el mismo tamaño? La respuesta está en la fuerza, ese concepto fundamental que gobierna prácticamente todo movimiento en el universo, desde el vuelo de un avión hasta el simple acto de caminar.

La física, esa asignatura que a veces nos quita el sueño, se vuelve mucho más comprensible cuando entendemos bien el concepto de fuerza. Y es que, seamos sinceros, calcular fuerzas no siempre resulta intuitivo. Muchos estudiantes de secundaria y bachillerato se enfrentan a problemas que les parecen imposibles de resolver… hasta que descubren las claves adecuadas.

En este artículo vamos a desentrañar este concepto desde sus raíces. Exploraremos las fórmulas principales para calcular diferentes tipos de fuerzas, resolveremos problemas paso a paso y, lo más importante, intentaremos que todo esto tenga sentido para ti, sea cual sea tu nivel de conocimientos previos.

El concepto de fuerza: Más allá de la simple definición

Antes de sumergirnos en fórmulas y cálculos, es fundamental comprender qué es realmente una fuerza. La definición clásica nos dice que una fuerza es toda causa capaz de modificar el estado de reposo o movimiento de un cuerpo, o de producir en él una deformación. Pero esta definición, aunque correcta, apenas araña la superficie.

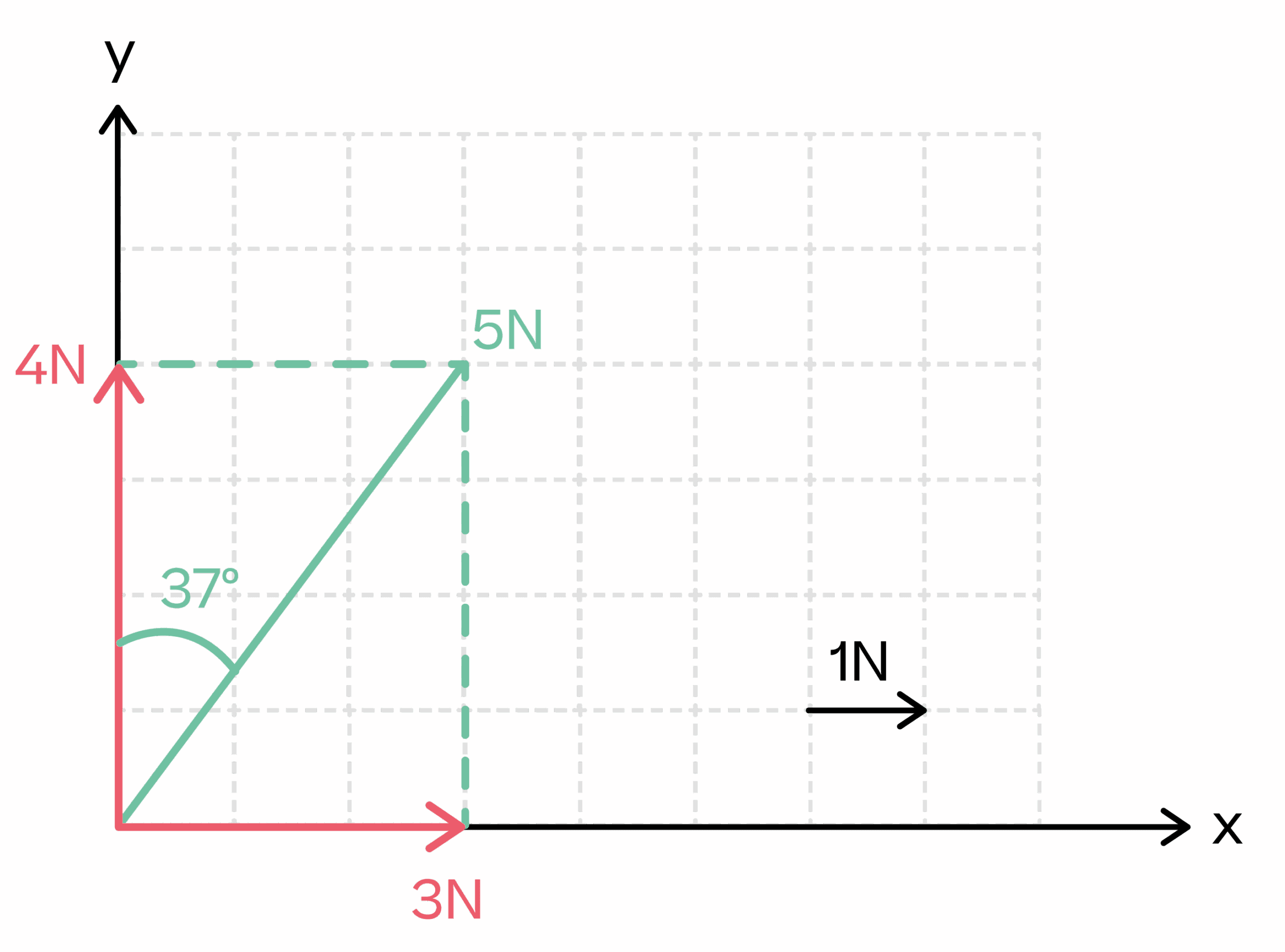
La fuerza es una magnitud vectorial, lo que significa que tiene tanto módulo (valor numérico) como dirección y sentido. Esta característica es crucial y explica por qué, por ejemplo, dos personas tirando de una cuerda en sentidos opuestos pueden anular sus esfuerzos mutuamente. No basta con saber «cuánta» fuerza se aplica, sino también «hacia dónde» se dirige.

En el Sistema Internacional (SI), la unidad de fuerza es el newton (N), en honor al físico Isaac Newton. Un newton equivale a la fuerza necesaria para proporcionar una aceleración de 1 m/s² a un objeto de 1 kg de masa.

Las Leyes de Newton: El Fundamento del Cálculo de Fuerzas

Cualquier estudio serio sobre fuerzas debe partir de las leyes de Newton. Estas tres leyes, formuladas en el siglo XVII, siguen siendo la base para resolver la inmensa mayoría de problemas de mecánica clásica.

Primera Ley: Principio de inercia

«Todo cuerpo persevera en su estado de reposo o movimiento rectilíneo uniforme a menos que sea obligado a cambiar su estado por fuerzas impresas sobre él.»

Esta ley nos dice que si la suma de todas las fuerzas que actúan sobre un objeto es cero, éste mantendrá su estado de movimiento (o reposo). ¿Qué significa esto para nuestros cálculos? Que cuando un sistema está en equilibrio, podemos plantear ecuaciones igualando la suma de fuerzas a cero:

∑F = 0

Segunda Ley: Principio fundamental de la finámica

«El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime.»

Esta es quizá la ley más importante para el cálculo de fuerzas, y se expresa mediante la conocida fórmula:

F = m·a

Donde:

• F es la fuerza resultante (N)
• m es la masa del objeto (kg)
• a es la aceleración producida (m/s²)

Esta ecuación es la que utilizaremos más frecuentemente en nuestros problemas.

Tercera Ley: Principio de acción y reacción

«Con toda acción ocurre siempre una reacción igual y contraria.»

Esta ley nos recuerda que las fuerzas siempre aparecen en pares. Si empujas una pared con una fuerza de 50 N, la pared te empuja a ti con 50 N en sentido contrario. Este principio es fundamental para resolver problemas donde interactúan varios cuerpos.

Tipos de fuerzas y sus fórmulas

Ahora que comprendemos los fundamentos, vamos a explorar los diferentes tipos de fuerzas que encontraremos en problemas típicos de física, junto con sus respectivas fórmulas.

Fuerza gravitatoria (Peso)

El peso es la fuerza con que la Tierra (u otro cuerpo celeste) atrae a los objetos. Su fórmula es:

P = m·g

Donde:

• P es el peso (N)
• m es la masa del objeto (kg)
• g es la aceleración de la gravedad (9,8 m/s² en la superficie terrestre)

Fuerza normal

La fuerza normal es aquella que ejerce una superficie sobre un objeto que está apoyado en ella, en dirección perpendicular a la superficie. En una superficie horizontal, si no hay otras fuerzas verticales además del peso:

N = m·g

Sin embargo, en planos inclinados o cuando hay otras fuerzas verticales, la normal debe calcularse mediante el equilibrio de fuerzas en el eje vertical.

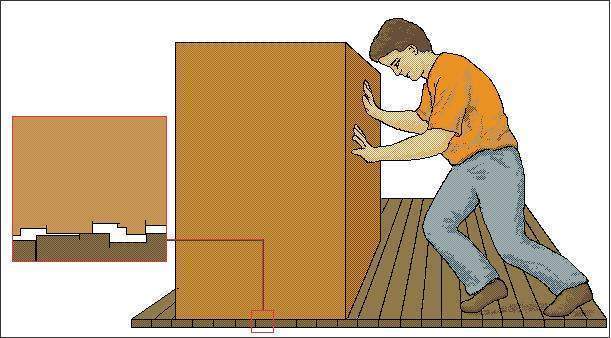
Fuerza de rozamiento

La fuerza de rozamiento se opone al movimiento relativo entre dos superficies en contacto. Para el rozamiento por deslizamiento:

Fr = μ·N

Donde:

• Fr es la fuerza de rozamiento (N)
• μ es el coeficiente de rozamiento (adimensional)
• N es la fuerza normal (N)

El coeficiente μ puede ser estático (μₑ) cuando el objeto está en reposo, o dinámico (μₖ) cuando está en movimiento, siendo generalmente μₑ > μₖ.

Fuerza elástica (Ley de Hooke)

Cuando un muelle (o resorte) se estira o comprime, ejerce una fuerza proporcional a su deformación:

F = -k·x

Donde:

• F es la fuerza elástica (N)
• k es la constante elástica del muelle (N/m)
• x es la deformación respecto a la posición de equilibrio (m)
• El signo negativo indica que la fuerza se opone a la deformación

Tensión

La tensión es la fuerza que soporta una cuerda, cable o similar cuando es sometida a fuerzas que tienden a estirarla. En una cuerda ideal (masa despreciable y no extensible), la tensión es la misma en todos sus puntos.

Fuerza centrípeta

Es la fuerza que mantiene a un objeto en movimiento circular:

Fc = m·v²/r

Donde:

• Fc es la fuerza centrípeta (N)
• m es la masa (kg)
• v es la velocidad tangencial (m/s)
• r es el radio de la trayectoria circular (m)

Estrategias para resolver problemas de fuerzas

Antes de lanzarnos a resolver ejemplos concretos, es útil establecer una metodología general para abordar problemas de fuerzas:

1. Identifica todas las fuerzas que actúan sobre cada objeto del problema.
2. Dibuja un diagrama de cuerpo libre para cada objeto, representando todas las fuerzas con vectores.
3. Establece un sistema de coordenadas (normalmente cartesiano) y descompón las fuerzas en sus componentes x e y.
4. Aplica la segunda ley de Newton en cada eje:
   • ∑Fx = m·ax
   • ∑Fy = m·ay
5. Resuelve el sistema de ecuaciones resultante.

Con esta estrategia en mente, vamos a resolver algunos problemas típicos que te puedes encontrar en secundaria y bachillerato.

Problemas resueltos de cálculo de fuerzas

Problema 1: Fuerza y aceleración en un plano horizontal

Enunciado: Un objeto de 5 kg está sobre una superficie horizontal sin rozamiento. Se le aplica una fuerza horizontal constante de 15 N. Calcular: a) La aceleración del objeto. b) La velocidad después de 4 segundos, partiendo del reposo. c) La distancia recorrida en esos 4 segundos.

Solución:

a) Aplicando la segunda ley de Newton: F = m·a a = F/m = 15 N / 5 kg = 3 m/s²

b) Como la aceleración es constante, podemos usar la ecuación: v = v₀ + a·t v = 0 + 3 m/s² · 4 s = 12 m/s

c) Para la distancia recorrida: x = v₀·t + (1/2)·a·t² x = 0 + (1/2) · 3 m/s² · (4 s)² = 24 m

Problema 2: Objeto en un plano inclinado con rozamiento

Enunciado: Un bloque de 2 kg se encuentra en reposo sobre un plano inclinado 30° respecto a la horizontal. El coeficiente de rozamiento estático entre el bloque y el plano es μₑ = 0,4. Determinar: a) Si el bloque permanecerá en reposo o comenzará a deslizar. b) En caso de deslizar, calcular su aceleración.

Solución:

a) Primero identificamos las fuerzas:

• Peso (P = m·g = 2 kg · 9,8 m/s² = 19,6 N)
• Normal (N)
• Fuerza de rozamiento estático (Fr = μₑ·N)

Descomponemos el peso en sus componentes paralela y perpendicular al plano:

• Componente perpendicular: P⊥ = P·cos(30°) = 19,6 N · 0,866 = 16,97 N
• Componente paralela: P∥ = P·sen(30°) = 19,6 N · 0,5 = 9,8 N

La normal es igual a la componente perpendicular del peso: N = P⊥ = 16,97 N

La máxima fuerza de rozamiento estático posible es: Fr,máx = μₑ·N = 0,4 · 16,97 N = 6,79 N

Como la componente paralela del peso (9,8 N) es mayor que la máxima fuerza de rozamiento estático (6,79 N), el bloque comenzará a deslizar.

b) Al deslizar, actúa el rozamiento dinámico (supongamos μₖ = 0,3): Fr = μₖ·N = 0,3 · 16,97 N = 5,09 N

La fuerza resultante en dirección del plano será: F = P∥ – Fr = 9,8 N – 5,09 N = 4,71 N

Y la aceleración: a = F/m = 4,71 N / 2 kg = 2,36 m/s²

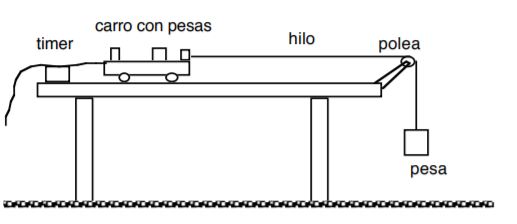
Problema 3: Sistema de dos cuerpos con polea

Enunciado: Dos masas, m₁ = 3 kg y m₂ = 5 kg, están conectadas por una cuerda que pasa por una polea sin fricción. La masa m₁ está sobre una mesa horizontal sin rozamiento, mientras que m₂ cuelga verticalmente. Calcular: a) La aceleración del sistema. b) La tensión en la cuerda.

Solución:

a) Identificamos las fuerzas en cada masa:

Para m₁:

• Peso (P₁ = m₁·g = 3 kg · 9,8 m/s² = 29,4 N)
• Normal (N = P₁ = 29,4 N)
• Tensión de la cuerda (T)

Para m₂:

• Peso (P₂ = m₂·g = 5 kg · 9,8 m/s² = 49 N)
• Tensión de la cuerda (T)

Aplicando la segunda ley de Newton:

• Para m₁ (eje x): T = m₁·a
• Para m₂ (eje y): P₂ – T = m₂·a

De la segunda ecuación: T = P₂ – m₂·a = 49 N – 5 kg·a

Sustituyendo en la primera: 49 N – 5 kg·a = 3 kg·a 49 N = 8 kg·a a = 49 N / 8 kg = 6,13 m/s²

b) Con la aceleración, calculamos la tensión: T = m₁·a = 3 kg · 6,13 m/s² = 18,39 N

O también: T = P₂ – m₂·a = 49 N – 5 kg · 6,13 m/s² = 18,35 N (La pequeña diferencia se debe a los redondeos)

Aplicaciones prácticas del cálculo de fuerzas

Puede que te preguntes: ¿y para qué me sirve todo esto? Pues bien, el cálculo de fuerzas no es solo un ejercicio académico. Tiene aplicaciones en numerosos campos:

• Ingeniería: diseño de estructuras, máquinas y sistemas mecánicos.
• Arquitectura: cálculo de cargas en edificios.
• Automoción: diseño de sistemas de frenado, suspensión, etc.
• Aeronáutica: estudio de la sustentación y resistencia aerodinámica.
• Medicina: biomecánica del cuerpo humano.
• Deportes: optimización de técnicas y equipamiento.

Incluso en tu vida diaria, entender las fuerzas te ayuda a comprender mejor el mundo que te rodea. ¿Por qué es más difícil empujar un carrito de la compra cuando está lleno? ¿Por qué resbalas más en hielo que en cemento? ¿Cómo funcionan los cinturones de seguridad? Todas estas preguntas encuentran respuesta en los principios que hemos explorado.

Errores comunes y cómo Evitarlos

A lo largo de mis años como profesor de física, he identificado algunos errores frecuentes que cometen los estudiantes al resolver problemas de fuerzas:

1. Olvidar que la fuerza es un vector: muchas veces se olvida considerar la dirección y sentido, trabajando solo con módulos.
2. No dibujar un diagrama de cuerpo libre: este paso es fundamental y ahorra muchos dolores de cabeza.
3. Confundir masa y peso: la masa es una propiedad intrínseca del cuerpo (kg), mientras que el peso es una fuerza (N).
4. No descomponer correctamente las fuerzas: especialmente en planos inclinados, es crucial descomponer las fuerzas en los ejes adecuados.
5. Ignorar fuerzas que actúan sobre el sistema: a veces se olvidan fuerzas como la normal o el rozamiento.

Si evitas estos errores y sigues la metodología propuesta, estarás en el buen camino para dominar el cálculo de fuerzas.

Herramientas y recursos para profundizar

Si quieres seguir practicando y aprendiendo sobre el cálculo de fuerzas, te recomiendo estos recursos:

• Simuladores físicos: PhET (University of Colorado) ofrece simulaciones interactivas excelentes.
• Aplicaciones móviles: «Physics Toolbox» te permite realizar experimentos con los sensores de tu móvil.
• Canales de YouTube: «Quantum Fracture» o «Date un Vlog» explican conceptos físicos de forma amena y rigurosa.
• Libros de problemas: «Física para la Ciencia y la Tecnología» de Tipler es un clásico para nivel de bachillerato y universidad.

Conclusión: dominando las fuerzas, dominando la física

Hemos recorrido un largo camino desde la definición básica de fuerza hasta la resolución de problemas complejos. Espero que ahora veas que el cálculo de fuerzas, aunque puede parecer intimidante al principio, se vuelve manejable cuando se aborda con una metodología clara y sistemática.

Recuerda que la física no es solo memorizar fórmulas, sino entender conceptos y saber aplicarlos. Las fuerzas son uno de los pilares fundamentales de esta ciencia, y dominarlas te abrirá las puertas a comprender muchos otros fenómenos naturales.

Como dijo el propio Newton: «Si he visto más lejos es porque estoy sentado sobre los hombros de gigantes». Cada problema que resuelvas te eleva un poco más, permitiéndote ver más lejos en el fascinante mundo de la física.

Y tú, ¿te atreves a seguir explorando las fuerzas que gobiernan nuestro universo?

Referencias bibliográficas

1. Tipler, P. A., & Mosca, G. (2010). Física para la ciencia y la tecnología (6ª ed.). Editorial Reverté.
2. Serway, R. A., & Jewett, J. W. (2018). Física para ciencias e ingeniería (10ª ed.). Cengage Learning.
3. Burbano de Ercilla, S., Burbano García, E., & Gracia Muñoz, C. (2015). Física General (32ª ed.). Editorial Tébar Flores.
4. Alonso, M., & Finn, E. J. (2018). Física. Addison-Wesley (Pearson Education).
5. Hewitt, P. G. (2016). Física Conceptual (12ª ed.). Pearson Education.
6. Página web PhET Interactive Simulations, Universidad de Colorado Boulder. https://phet.colorado.edu/es/simulations/filter?subjects=physics&type=html,prototype