Después de más de quince años explicando física en las aulas de secundaria, puedo asegurar que el Movimiento Rectilíneo Uniformemente Acelerado (MRUA) es uno de esos conceptos que, una vez comprendido, abre las puertas a toda la mecánica clásica. ¿Cuántas veces habéis visto cómo los estudiantes se quedan perplejos cuando un coche frena o cuando una pelota cae? La respuesta está en este fascinante tipo de movimiento.

El MRUA no es simplemente una fórmula más que memorizar para el examen. Es la base sobre la que se construye nuestra comprensión del mundo físico que nos rodea. Desde el momento en que Galileo observó las esferas rodando por planos inclinados hasta las misiones espaciales actuales, el movimiento uniformemente acelerado ha sido fundamental para describir cómo se mueven los objetos en nuestro universo.

¿Qué es el MRUA? Definición y Características

El Movimiento Rectilíneo Uniformemente Acelerado es aquel en el que un objeto se desplaza en línea recta con una aceleración constante. Esto significa que la velocidad del objeto cambia de manera uniforme a lo largo del tiempo.

Características principales del MRUA:

• Trayectoria rectilínea: El objeto se mueve en línea recta
• Aceleración constante: La aceleración no varía con el tiempo (a ≠ 0)
• Velocidad variable: La velocidad cambia de forma uniforme
• Puede ser acelerado o desacelerado: Dependiendo del signo de la aceleración

Un ejemplo cotidiano que siempre funciona en clase es el de un coche que arranca desde el semáforo. Al principio está parado (velocidad inicial = 0), pero va aumentando su velocidad de manera constante hasta alcanzar la velocidad deseada. ¡Ahí tenemos nuestro MRUA en acción!

Las Ecuaciones del MRUA: Herramientas Fundamentales

Ecuaciones cinemáticas básicas

El MRUA se describe mediante cuatro ecuaciones fundamentales que relacionan las magnitudes físicas involucradas:

1. Ecuación de la velocidad:

v = v₀ + a·t

2. Ecuación de la posición:

x = x₀ + v₀·t + ½·a·t²

3. Ecuación velocidad-posición:

v² = v₀² + 2·a·(x - x₀)

4. Ecuación de la velocidad media:

v_media = (v₀ + v)/2

Donde:

• v: velocidad final (m/s)
• v₀: velocidad inicial (m/s)
• a: aceleración (m/s²)
• t: tiempo (s)
• x: posición final (m)
• x₀: posición inicial (m)

¿Cuándo usar cada ecuación?

Esta es la pregunta del millón que me hacen mis estudiantes. La clave está en identificar qué datos conocemos y qué queremos calcular:

• Si conocemos tiempo y queremos velocidad → Ecuación 1
• Si conocemos tiempo y queremos posición → Ecuación 2
• Si NO conocemos tiempo pero sí velocidades y distancia → Ecuación 3

Tipos de MRUA: Acelerado vs Desacelerado

MRUA Acelerado (a > 0)

Cuando la aceleración tiene el mismo sentido que la velocidad, el móvil acelera. Un ejemplo típico es una pelota que rueda cuesta abajo por una pendiente.

MRUA Desacelerado o Retardado (a < 0)

Cuando la aceleración tiene sentido contrario a la velocidad, el móvil desacelera. Pensad en un coche que frena: la velocidad disminuye porque la aceleración es negativa.

Casos especiales: Caída libre y lanzamiento vertical

La caída libre es el ejemplo más puro de MRUA. Todos los objetos caen con la misma aceleración (g = 9,8 m/s²), independientemente de su masa. ¡Galileo tenía razón cuando dejó caer objetos desde la Torre de Pisa!

MRUA Ejercicios Resueltos: Práctica Paso a Paso

Ejercicio 1: Arranque de un vehículo

Enunciado: Un coche arranca desde el reposo y alcanza una velocidad de 72 km/h en 8 segundos. Calcular: a) La aceleración del vehículo b) La distancia recorrida en esos 8 segundos

Resolución:

Primero, convertimos las unidades:

• v₀ = 0 m/s (parte del reposo)
• v = 72 km/h = 72 × (1000/3600) = 20 m/s
• t = 8 s

a) Cálculo de la aceleración: Usando v = v₀ + a·t 20 = 0 + a·8 a = 20/8 = 2,5 m/s²

b) Cálculo de la distancia: Usando x = x₀ + v₀·t + ½·a·t² x = 0 + 0·8 + ½·2,5·8² x = 0 + 0 + 1,25·64 = 80 m

Ejercicio 2: Frenado de emergencia

Enunciado: Un vehículo circula a 90 km/h cuando el conductor observa un obstáculo y frena con una deceleración de 6 m/s². ¿Qué distancia necesita para detenerse completamente?

Resolución:

Datos:

• v₀ = 90 km/h = 25 m/s
• v = 0 m/s (se detiene)
• a = -6 m/s² (negativa porque frena)

Como no conocemos el tiempo pero sí las velocidades, usamos: v² = v₀² + 2·a·(x – x₀)

0² = 25² + 2·(-6)·x 0 = 625 – 12x 12x = 625 x = 52,08 m

Ejercicio 3: Caída libre desde una altura

Enunciado: Desde lo alto de un edificio de 45 m de altura se deja caer una pelota. Calcular: a) El tiempo que tarda en llegar al suelo b) La velocidad con que impacta

Resolución:

Datos:

• h = 45 m
• v₀ = 0 m/s (se deja caer)
• g = 9,8 m/s² (aceleración de la gravedad)

a) Tiempo de caída: Usando h = v₀·t + ½·g·t² 45 = 0 + ½·9,8·t² 45 = 4,9·t² t² = 45/4,9 = 9,18 t = 3,03 s

b) Velocidad de impacto: Usando v = v₀ + g·t v = 0 + 9,8·3,03 v = 29,7 m/s

Gráficas del MRUA: Interpretación Visual

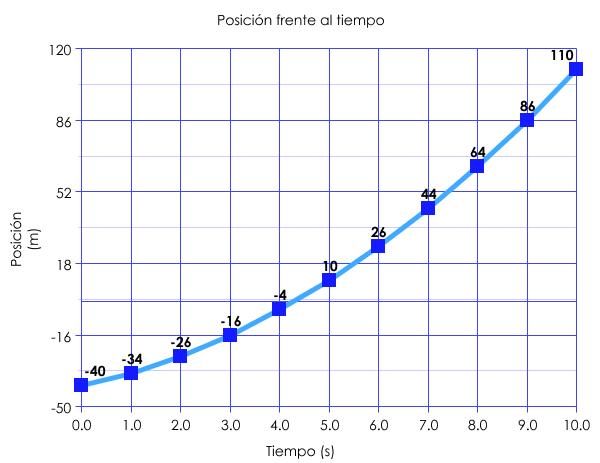
Gráfica posición-tiempo (x-t)

En el MRUA, la gráfica x-t es una parábola. La pendiente de la tangente en cualquier punto nos da la velocidad instantánea en ese momento.

Gráfica velocidad-tiempo (v-t)

La gráfica v-t es una línea recta cuya pendiente representa la aceleración. El área bajo la curva nos proporciona el desplazamiento.

Gráfica aceleración-tiempo (a-t)

En el MRUA, la aceleración es constante, por lo que la gráfica a-t es una línea horizontal.

Aplicaciones Prácticas del MRUA

En la vida cotidiana

El MRUA está presente en multitud de situaciones:

• Arranque y frenado de vehículos.
• Caída de objetos.
• Lanzamientos verticales.
• Movimiento en ascensores.
• Deportes (salto de altura, lanzamiento de peso).

En la ingeniería y tecnología

Los ingenieros utilizan las ecuaciones del MRUA para:

• Diseñar sistemas de frenado.
• Calcular distancias de seguridad.
• Planificar trayectorias de cohetes.
• Optimizar el rendimiento de vehículos.

Errores Comunes en MRUA

Error 1: Confundir velocidad con aceleración

Muchos estudiantes piensan que si un objeto se mueve rápido, tiene mucha aceleración. ¡Falso! La aceleración es el cambio de velocidad, no la velocidad en sí.

Error 2: Olvidar las unidades

Siempre, siempre hay que trabajar con unidades coherentes. Si usamos metros, trabajamos con segundos y m/s².

Error 3: No considerar el signo de la aceleración

El signo de la aceleración indica su sentido. Una aceleración negativa no significa que el objeto vaya hacia atrás, sino que la aceleración tiene sentido opuesto al movimiento.

Estrategias para Resolver Problemas de MRUA

Método sistemático

1. Leer cuidadosamente el enunciado
2. Identificar los datos conocidos y desconocidos
3. Elegir la ecuación apropiada
4. Sustituir valores y calcular
5. Verificar que el resultado tenga sentido físico

Consejos de una profesora experimentada

Después de tantos años enseñando, he comprobado que los estudiantes que mejor comprenden el MRUA son aquellos que:

• Visualizan el problema mentalmente
• Dibujan esquemas cuando es posible
• Comprueban siempre las unidades
• Practican con ejercicios variados

Conexión con Otros Conceptos Físicos

El MRUA no es un concepto aislado. Se conecta directamente con:

• Dinámica: Las fuerzas causan aceleraciones (2ª Ley de Newton).
• Energía: La energía cinética depende de la velocidad.
• Movimiento circular: Aceleración centrípeta.
• Ondas: Movimiento armónico simple.

Conclusión

El Movimiento Rectilíneo Uniformemente Acelerado es mucho más que un conjunto de ecuaciones matemáticas. Es la puerta de entrada a la comprensión del mundo físico que nos rodea. Desde el simple gesto de soltar un objeto hasta los complejos cálculos necesarios para enviar una sonda espacial a Marte, el MRUA está presente en innumerables situaciones.

Como profesora, he visto cómo estudiantes que inicialmente se sentían intimidados por las ecuaciones del MRUA acababan desarrollando una verdadera pasión por la física. La clave está en entender que detrás de cada fórmula hay una descripción elegante y precisa de cómo se comporta la naturaleza.

Espero que esta guía os haya resultado útil y que os ayude a comprender mejor este fascinante concepto. Recordad: la física no es solo memorizar fórmulas, sino entender cómo funciona el mundo que nos rodea. ¡Y el MRUA es un excelente punto de partida para esa aventura!

---

Referencias Bibliográficas

1. Tipler, P. A., & Mosca, G. (2010). Física para la ciencia y la tecnología. Editorial Reverté.
2. Serway, R. A., & Jewett, J. W. (2014). Physics for Scientists and Engineers. Cengage Learning.
3. Resnick, R., Halliday, D., & Krane, K. S. (2002). Física Volumen 1. Editorial Continental.
4. Ministerio de Educación, Cultura y Deporte. (2015). Real Decreto 1105/2014, de 26 de diciembre, por el que se establece el currículo básico de la Educación Secundaria Obligatoria y del Bachillerato. BOE. [https://www.boe.es/eli/es/rd/2014/12/26/1105]
5. Instituto Nacional de Tecnologías Educativas y de Formación del Profesorado. (2021). Recursos educativos de Física y Química. [https://intef.es/]